Манипулирование данными
Существует формализованный математический аппарат (набор операций), который позволяет формализованно описать манипулирование данными – реляционная алгебра. Она является математическим оператором, реализованным средствами SQL. Реляционная алгебра применима только к реляционным БД, где данные хранятся в виде отношений (была предложена Дж.Коддом (J.Codd)).
Реляционная алгебра – перечень операций, применимых к отношениям, эти операции можно разделить на 2 класса:
  • Унарные операции. Операции над одним отношением;
  • Бинарные операции. Операции над двумя отношениями;
Реляционная алгебра Кодда включает 8 операций над отношениями:
  • 2 унарные: проекция и выборка;
  • остальные – бинарные: объединение, пересечение, разность, деление, соединение, декартово произведение.
Кларус Дейт добавил ещё 5 новых операций:
  • 3 унарные операции: расширение, обобщение, переименование;
  • 2 бинарные операции: полусоединение, полувычитание.
: при этих операциях у двух отношений заголовки должны быть одинаковыми.

Аспирант (R1)
Табельный номер Фамилия Имя Отчество Год рождения Пол
14 Алексеев Пётр Валерьевич 1984 М
28 Георгадзе Шота Шавлович 1982 М
29 Ахметова Зульфия Равильевна 1983 Ж

Преподаватель (R2)
Табельный номер Фамилия Имя Отчество Год рождения Пол
28 Георгадзе Шота Шавлович 1982 М
185 Андреев Владислав Николаевич 1968 М
206 Абрамян Софья Борисовна 1956 Ж
83 Ильиченко Владимир Иванович 1948 М

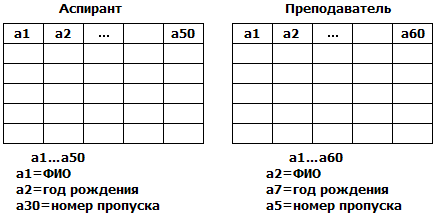
Объединение (UNION). R = R1 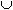R2 – результирующее отношение содержит все кортежи исходных отношений R1 ­ и R2. Каждый кортеж входит в результирующее отношение только один раз. Результат объединения – таблица. Аспиранты и преподаватели = Аспирант 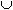Преподаватель.
Разность (DIFFERENCE, MINUS). R = R1 – R2. Итоговый результат – то, что содержится в R1 и не содержится в R2, т.е. Аспиранты, которые не занимаются преподаванием = Аспирант – Преподаватель.

(R)
Табельный номер Фамилия Имя Отчество Год рождения Пол
14 Алексеев Пётр Валерьевич 1984 М
29 Ахметова Зульфия Равильевна 1983 Ж

Пересечение (INTERSECTION). R = R1 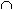 R2 – результирующее отношение содержит только те кортежи, которые имеются в обоих исходных отношениях R1 и R2. Аспиранты, которые преподают = Аспирант 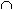Преподаватель.
Графическая реализация:
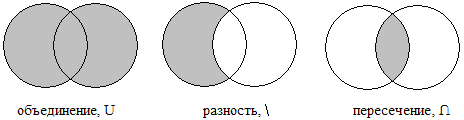
Объединение, разность, пересечение
Правила:
  1. Исходные отношения должны иметь одинаковую схему (число и порядок полей);
  2. Если отношения имеют разные схемы, но есть одинаковые поля (есть подмножество идентичных полей), то эти операции (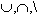) применяются к проекциям данных отношений на данные подмножества;
  3. Если имеются идентичные поля, но у них разные названия, то допустима операция переименования.
Унарные операции – операции над одним отношением:
  1. Выборка - выделение нужных строк, кортежей;
  2. Проекция - выделение нужных столбцов, атрибутов.
№ зачётной книжки Фамилия И.О. Год рождения Пол
1393 Иванов А.В. 1989 М
1862 Акопов Э.В. 1990 М
1864 Васильева Е.Ф. 1986 Ж
2341 Савицкий В.Б. 1988 М

Выборка (селекция, отбор, ограничение) обозначается σC(R). Выделяются только те кортежи, удовлетворяющие данному условию «С» – критерию выборки, фильтру. Условие – сколь угодно сложная логическая операция (выражение), которое включает в себя логические операции «И» и/или «ИЛИ».
Пример: студенты старше 1990 года рождения мужского пола = σгод рождения < 1990 AND Пол = «М».
Студент
№ зачётной книжки Фамилия И.О. Год рождения Пол
1393 Иванов А.В. 1989 М
2341 Савицкий В.Б. 1988 М

Проекция. a1, …, an – атрибуты. Результирующее отношение, содержит только перечисленные поля исходного отношения. Обозначается: 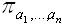(R).
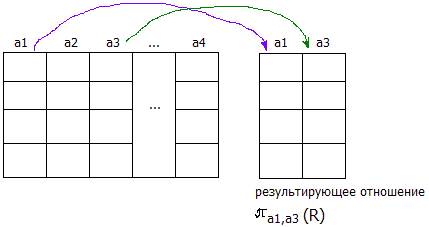
Пример
Пример: 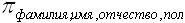(студент).

Фамилия И.О. Пол
Иванов А.В. М
Акопов Э.В. М
Васильева Е.Ф. Ж
Савицкий В.Б. М

Для чего используется?
  1. Для того, чтобы дать пользователю ту информацию, которая ему нужна;
  2. Обеспечивает операци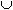и  и 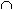над отношениями с разным количеством атрибутов.
Пример

Бинарные операции. Декартово произведение и соединение.

Студент
№ зачётной книжки Фамилия И.О. № комнаты
1393 Иванов А.В. 321
- - NULL
1864 Васильева Е.Ф. 321
2341 Савицкий В.Б. 321
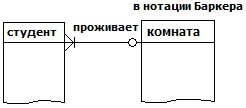
В нотации Баркера

Комната в общежитии
№ комн. Вместимость Площадь, м²
321 2 12
322 3 18
521 2 12

Дисциплина
Шифр Название Трудоёмкость
ОПД.Ф.10 БД 136
СД.Ф.10 ПАСОИУ 170

Предположим, что студенты из одного курса с одной специальности.

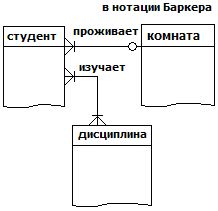
В нотации Баркера
Декартово произведение (R1 · R2) – бинарная операция, в которой участвуют 2 отношения. Результирующее отношение (R) состоит из кортежей, каждый из которых представляет собой слияние (сцепление, конкатенацию) кортежа из первого отношения с кортежем из второго отношения. Схема R получается суммированием исходных отношений.

Студент · дисциплина
№ зачётной книжки Фамилия И.О. № комнаты Шифр Название Трудоёмкость
1393 Иванов А.В. 321 ОПД.Ф.10 БД 136
1393 Иванов А.В. 321 СД.Ф.10 ПАСОИУ 170
1862 Акопов Э.В. NULL ОПД.Ф.10 БД 136
1862 Акопов Э.В. NULL СД.Ф.10 ПАСОИУ 170
1864 Васильева Е.Ф. 321 ОПД.Ф.10 БД 136
1864 Васильева Е.Ф. 321 СД.Ф.10 ПАСОИУ 170
2341 Савицкий В.Б. 321 ОПД.Ф.10 БД 136
2341 Савицкий В.Б. 321 СД.Ф.10 ПАСОИУ 170

Каждому студенту сопоставлены все дисциплины. Итого: 8 шт. кортежей.

№ зачётной книжки Название
1393 БД
1393 ПАСОИУ
1862 БД
1862 ПАСОИУ
1864 БД
1864 ПАСОИУ
2341 БД
2341 ПАСОИУ
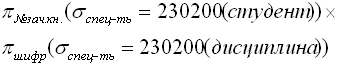
Операция декартового произведения не может применяться к отношениям, имеющим одинаковые поля. В этом случае они должны быть предварительно переименованы.

← Ctrl  Предыдущая  •  Следующая  Ctrl →
Сайт управляется системой uCoz